벌써 혼공단이 절반이 지났다. 그말인 즉, 개강도 절반밖에 남지 않았단 소리다.
왜 시간은 이렇게 야속하게 흐르는가. 조금은 천천히 흘러도 괜찮을 것 같은데,
꼭 시간은 눈치가 없는지 쉴땐 빠르게가고 일하거나 공부할땐 천천히 가는지 잘 모르겠다.
점점 공부한 것을 기록으로 남기는데, 회차를 거듭하다보니 점점 기록에 체계가 잡혀간다.
그러면서 점점 분량도 많아지고 난이도도 어려워지는 상황에서 나름 체계가 공부에 도움이 되는 것 같다.
(족장님 보고있나, 족장님이 공지로 어렵게 던진다는 교재 진도 저는 해냈습니다.)
3주차에는 효율적인 데이터 분석을 위해, 데이터를 정제하는 방법에 대해 집중적으로 다루었다. 이번에는 데이터가 가진 특징을 파악해보고자 한다.
1. 통계로 요약하기
'통계' 한번쯤은 들어보았을것이다. 다들 통계라 하면 수학이라고 생각해서, 통계라는 말을 들으면 벌써부터 착잡할 것이다. 하지만 그리 어렵지는 않다.
(물론 깊게 공부한다면 어려워 죽을지도 모른다, 필자는 전공이 수학교육이라 통계학 배울때 힘겨웠던 기억이 있다.)
어떠한 정보를 요약하여 파악하기 위해서는 통계가 필수적이다. 왜냐하면 우리는 일일히 분석을 하면서 데이터를 하나하나 읽어볼 시간도 없을 뿐더러, 그것은 매우 체력적으로 힘든 일이기 때문이다. 그래서 우리에게는 3줄요약처럼 간단하게파악할 수 있는 정보가 필요한데, 그 정보가 바로 통계라는 것이다.
통계를 딥하게 들어가면 분포니 뭐니 하는 이야기들이 있지만, 여기서는 우리가 자주 들어보았던 평균, 분산, 표준편차 들의 이야기를 다루어 볼 것이다. 교재에서는 각 통계량을 구해보면서 이야기하지만, 코딩을 하기전에 통계량의 의미부터 살펴본 뒤 가면 더 좋은 이야기가 될 것이므로, 통계량들의 특징부터 알아보자.
( tmi. 필자의 전공은 '수학교육'이므로 이에 대한 수학적 이론을 쉽고 쌈뽕하게 해보겠다.)
(1) 기술통계량의 정의 (+ 추가숙제)
어떤 정보들을 한번에 파악하려면, 요약본이 필요하다. 이 요약본이 바로 '기술통계'라고 생각하면 된다. 데이터가 가진 여러가지 특성을 정량적인 수치로 보여준다. 이때, 각 수학 정의나 계산식에 따라 구해진 값을 '통계량' 이라고 하는데 요약본에 주로 활용되는 통계량을 '기술통계량' 이라 생각하면 쉽다. 주로 이러한 기술통계량은 '평균', '최빈값', ' 중앙값' 등의 대푯값들과 산포도인 분산, 표준편차 외에도 최댓값, 최솟값, 분위수 등을많이 사용한다.
- 대푯값
: 말 그대로 어떤 데이터나 집단 등의 특성을 잘보여주는, 즉 데이터를 대표하는 값이라고 생각하면 된다. 대푯값으로는 평균, 최빈값, 중앙값 등이 있다.
1) (산술)평균 "Mean"
: 우리가 익숙하게 아는 평균은 사실 모든 데이터 값을 더한 뒤, 데이터의 개수로 나눈 값을 말한다. 이 값은 각 데이터의 값들이 평균값과 차이가 크지 않을 때, 즉, 편차가 작아질수록 데이터의 특징을 잘 나타내는 특징이 있다.
$$ m=\frac{1}{n}\sum_{k=1}^{n}x_k $$
2) 최빈값 "Mode"
: 데이터의 값들 중에서 가장 많은 빈도의 값. 쉽게 말하면, 데이터들 중에서 가장 많이 등장하는 숫자를 말한다. 평균의 경우 계산값이므로 데이터가 수치여야 하지만, 최빈값은 데이터의 빈도를 따지므로 숫자, 문자 모두 가능하다.
3) 중앙값 "Median"
: 데이터의 값을 크기순으로 나열 하였을때, 정중앙에 오는 값을 말한다. 중앙값을 구하기 위해서는 데이터는 대소비교가 가능한 경우에만 가능하다.
- 분위수
분위수란 크기순으로 나열한 후 일정한 간격으로 데이터를 쪼개어 구간을 만들 때, 경계에 있는 값을 말한다. 주로 사분위수를 많이 사용하는데, 사분위수는 데이터를 크기순으로 나열한 뒤 4등분하여 각 25%, 50%, 75% 경계에 있는 값을 말한다.
- 최댓값, 최솟값
최댓값(maximum), 최솟값(minimum)은 말그대로 데이터들 중에서 가장 큰 값과 작은 값을 말한다.
- 산포도
: 데이터(변량)이 어떤 기준으로 부터 얼마나 흩어져지에 대한 척도이다. 대푯값들을 구하더라도, 실제 데이터의 값들이 대푯값과 차이가 많이 난다면 의미가 없다. 그렇기 때문에 대푯값들이 얼마나 실제 데이터값과 얼마나 차이가 나는지에 대한 정보를 같이 제시해주어야하는데, 이 값이 바로 산포도이다. 대표적으로, 평균과 실제 데이터간의 차이를 설명하는 산포도로 분산과 표준편차가 있다.
1) 분산 "Variance"
: 단어의 뜻대로, 흩어진 정도를 말한다. 이때, 분산은 "평균으로부터 얼마나 떨어져있는가?"를 이야기한다. 즉, 대푯값 중 평균이 얼마나 실제 데이터를 잘 대표하는 지를 알려주는 값이다. 분산은 수학에서 "편차의 제곱의 평균"으로 정의하며, 이때 편차는 실제 데이터값에서 평균를 뺀 값을 말한다.
$$\sigma ^{2}=\frac{\sum_{k=1}^{n}(x_k-m)^{2}}{n}$$
이때, 분산의 값이 커지면 커질수록 평균으로부터 데이터들이 많이 떨어져있다. 즉, 평균과 실제데이터들 간의 차이가 크다.
2) 표준편차 "Standard Deviation"
: 분산에 제곱근을 씌워 구한 값이다. 표준편차는 분산과 제곱근의 차이밖에 없어 차이가 없어 보일 수 있지만, 분산은 단지 평균으로부터 얼마나 각 실제 데이터들이 떨어져있는 가를 설명한다면, 표준편차는 전체적인 데이터가 어떻게 흩어져있는가에 대한 분포를 알려준다고 생각하면 쉽다. 즉, 분산은 데이터 하나하나에 집중한다면, 표준편차는 전체적으로 데이터가 어떻게 흩어진지를 알려준다.
$$ \sigma = \sqrt{\frac{\sum_{k=1}^{n}(x_k-m)^{2}}{n}}$$
(2) 기술통계량 구하기
지금까지 기술통계량에 대한 이야기를 공부했으니, 본격적으로 이를 직접 파이썬을 활용하여 구해보고자 한다. 각 수학적 정의에 따라 코딩하여 구해도 되지만, 요즘은 이를 한번에 구해주는 메소드들이 잘 지원이 되고 있다. 대표적인 예시로 pandas 라이브러리에 describe() 메서드가 있다.
import gdown
import pandas as pd
gdown.download('https://bit.ly/3736JW1', 'ns_book6.csv', quiet=False)
ns_book6 = pd.read_csv('ns_book6.csv', low_memory=False)
ns_book6.head()
ns_book6.describe() # 해당 데이터프레임에서 수치형데이터를 가진 열들의 기술통계량을 출력한다.
describe() 메서드에는 기본적으로 수치형데이터를 가진 열별로 평균, 분산, 표준편차, 사분위수, 최댓값, 최솟값을 구하여 출력한다.
[출력결과]

기술통계량을 보니, 도서권수의 최솟값이 0이라고 보인다. 이말인 즉슨, 도서가 구비되어있지 않는데 대출은 진행된다는 소리인데 무엇인가 이상하다. 이런 경우에는 해당 데이터는 제외하거나 처리를 해야하는데 어떻게하는게 좋을까?
기본적으로, 이에 해당하는 상황이라면 분석에서 무시해도 괜찮을정도의 개수인지를 파악해야하는게 좋다. 만약 도서권수가 0인 데이터가 전체에 1%도 채 안된다면, 분석을 할때 삭제해도 큰 무리가 없을 것이다. 그러나 반대로 상당수의 책들이 0권이라면, 이를 섣불리 삭제하여 분석을 진행하면 결과에 문제가 생길 것이다. 하여 이를 확인하고 문제가 없다면, 제외시키자.
sum(ns_book6['도서권수']==0)
ns_book7= ns_book6[ns_book6['도서권수']>0][출력결과]

전체에 1%도 안되는 데이터가 도서권수가 0이다. 그러니 무시해도 괜찮을듯 하다.

만약, 각각 기술통계량을 따로 구하고싶다면 다음 메서드들을 활용하여 개별로 구할수도 있다.
| 통계량 | 메서드 |
| 평균 | .mean() |
| 중앙값 | .median() |
| 최솟값 | .min() |
| 최댓값 | .max() |
| 사분위수 | .quantile() |
| 분산 | .var() |
| 표준편차 | .std() |
| 최빈값 | .mode() |
2. 분포 요약하기
각 데이터를 수치로 한번에 파악하는 기술통계량에 대하여 살펴보았다. 그런데, 수치로만 보니 여전히 이해하기에는 조금 시간이 걸린다. 시각적인 그림으로 볼 수 있다면, 더욱 편하게 데이터를 파악할 수 있을텐데 좋은 방법이 없을까? 이는 파이썬에서 matplotlib 라이브러리가 대표적으로 사용된다.
(1) 산점도
산점도는 각 데이터를 좌표평면상에 점으로 나타내는 방법이다. 학창시절에 수학시간에 배웠던 x축과 y축으로 이루어진 좌표평면이 기억나는가? 바로 그 평면에 x축과 y축의 이름을 지정해주고 그것을 좌표처럼 점으로 찍어 보여주는 것이라고 보면 된다.
import matplotlib.pyplot as plt
# 만약 해당 라이브러리가 설치되어있지 않다면 pip 명령어로 라이브러리를 설치하면 된다.
# pip install matplotlib
# 작성일 기준, scatter()메서드는 matplotlib.pyplot을 호출해야 사용가능하다.
# 뿐만 아니라, hist(), boxplot() 메소드 전부 사용하기 위한 모듈 이름이 바뀌었다.
plt.scatter(ns_book7['번호'], ns_book7['대출건수'])
# 산점도를 그려주는 scatter() 메서드에 x축의 정보와 y축의 정보를 넘겨주면 자동으로 그려준다.
# 같은 좌표에 찍히는 데이터들의 밀집도를 보고싶다면, alpha 매개변수에 값을 지정하면 밀집된 정도에 따라 진하게 표시한다.
plt.show()
# 산점도를 그림으로 그려 반환한다.[출력결과]
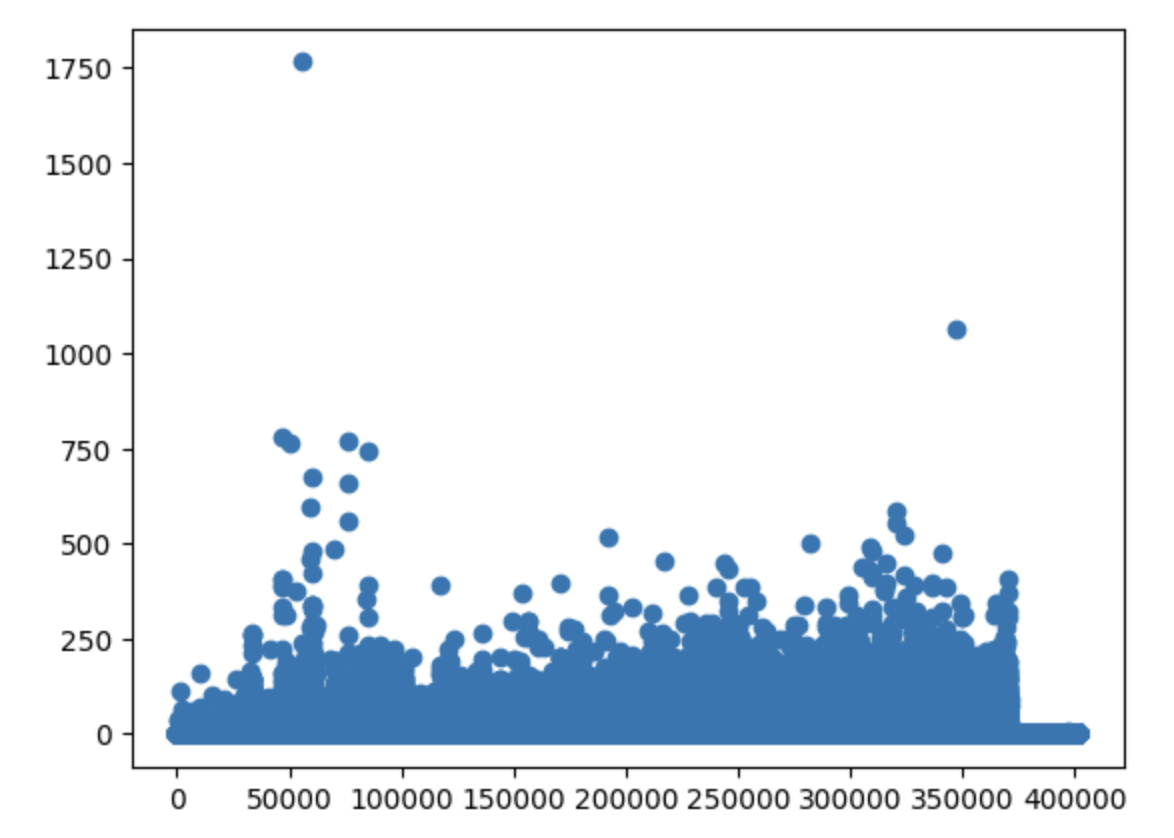
(2) 히스토그램
쉽게 설명하면 우리가 익히 아는 막대그래프라고 생각하면 된다. 조금 차이가 있다면, 히스토그램은 수치형데이터에서 일정한 구간을 나누어서 각 구간에 해당하는 데이터의 개수를 막대그래프로 표현해준다. 이 히스토그램을 표로 표현하는 도수분포표도 있다.
plt.hist(ns_book7['대출건수'], bins=100)
# 대출건수를 x축으로 하여 건수의 범위를 100개로 분할하여 히스토그램으로 그린다.
plt.yscale('log')
# 특정 구간의 데이터수가 너무 압도적으로 많아 다른 구간의 그래프가 보이지 않을때 사용한다.
# 즉, 값을 log를 취하여 숫자를 조금 작게 만든다.
plt.show()
[출력결과]

(3) 상자수염_box plot
상자수염이라고 불리는 box plot은 분위수에 따라 데이터를 상자모양으로 그려준다. 상자수염 그래프를 읽는 방법을 나중에 설명하기로 하고, 우선 이를 그려보자.
plt.boxplot(ns_book7[['대출건수', '도서권수']], whis=(0, 100))
# 데이터를 상자수염으로 그리기위한 기준열을 배열로 전달하여 그린다.
# 수염의 길이를 적절히 조절하려면 whis 매개변수에 길이를 지정하면 된다.
plt.yscale('log')
plt.show()[출력결과]

3. 기본숙제_ p.279 5번
5. ns_book7 남산도서관 대출데이터에서 1980~2022사이에 발행된 도서를 선택하여 다음과 같은 '발행년도' 열의 히스토그램을 그려보세요.
[답안]
selceted_rows = (1980<= ns_book7['발행년도']) & (ns_book7['발행년도']<=2022)
plt.hist(ns_book7.loc[selceted_rows, '발행년도'])
plt.show()
'혼자 공부하는 > 데이터분석 with Python' 카테고리의 다른 글
| [혼공분석] 6주차_복잡한 데이터 표현하기 (0) | 2025.02.23 |
|---|---|
| [혼공분석] 5주차_데이터 시각화하기 (1) | 2025.02.16 |
| [혼공분석] 3주차_데이터 정제하기 (0) | 2025.01.26 |
| [혼공분석] 2주차_데이터 수집하기 (0) | 2025.01.19 |
| [혼공분석] 1주차_데이터 분석을 시작하며 (0) | 2025.01.08 |